Part 3

Variations

B-Tree has different variations, improving different aspects of the base design. They all share a few things in common: tree structure, the balancing mechanism through splits and merges, and lookup/insert/delete algorithms. Other details, for instance, handling of concurrency, split/merge strategy, on-disk representations, maintenance processes, may vary between implementations. It’s impossible to go through all variations, so we will cover the most notable ones.

B+ Tree

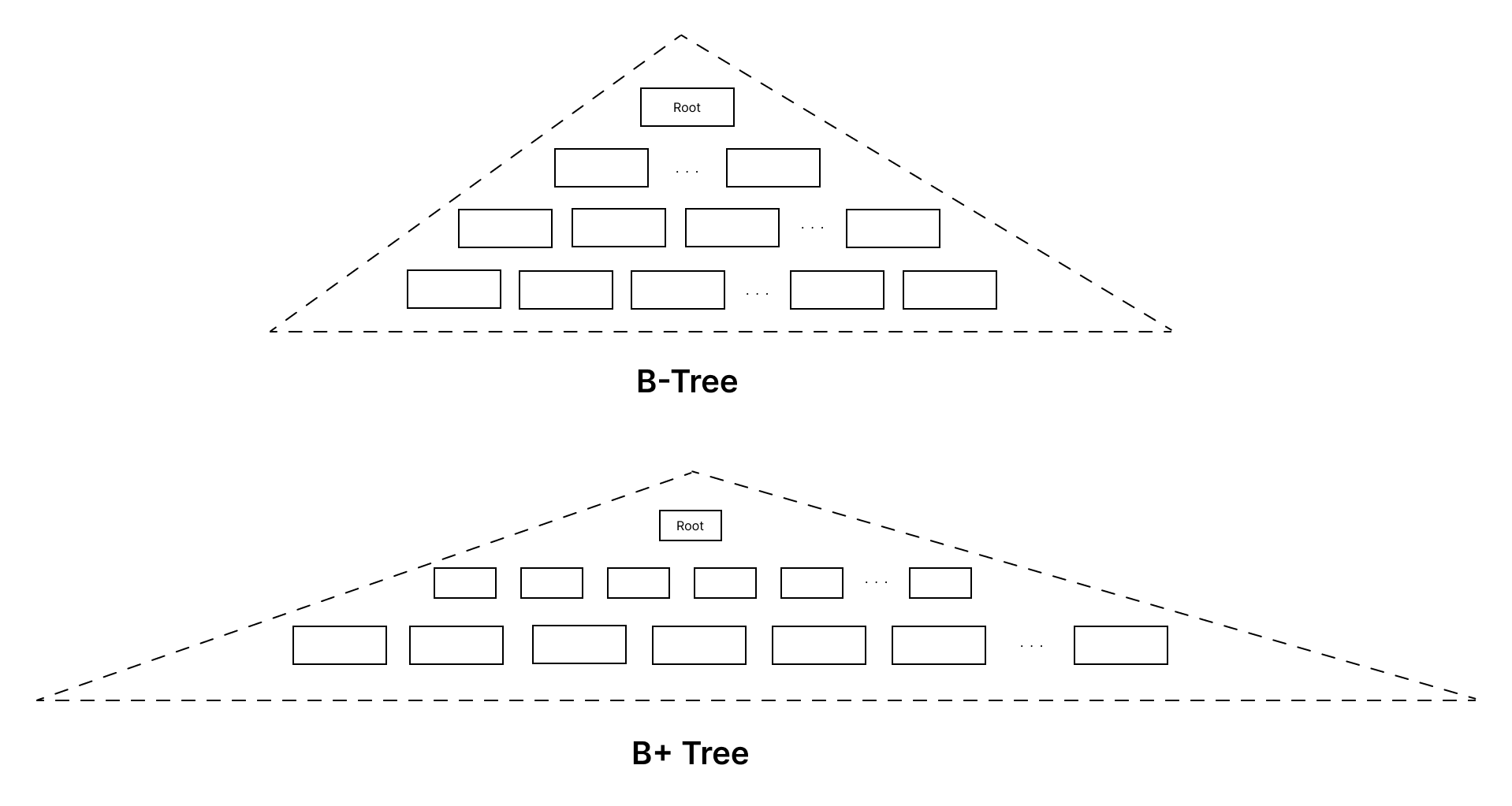
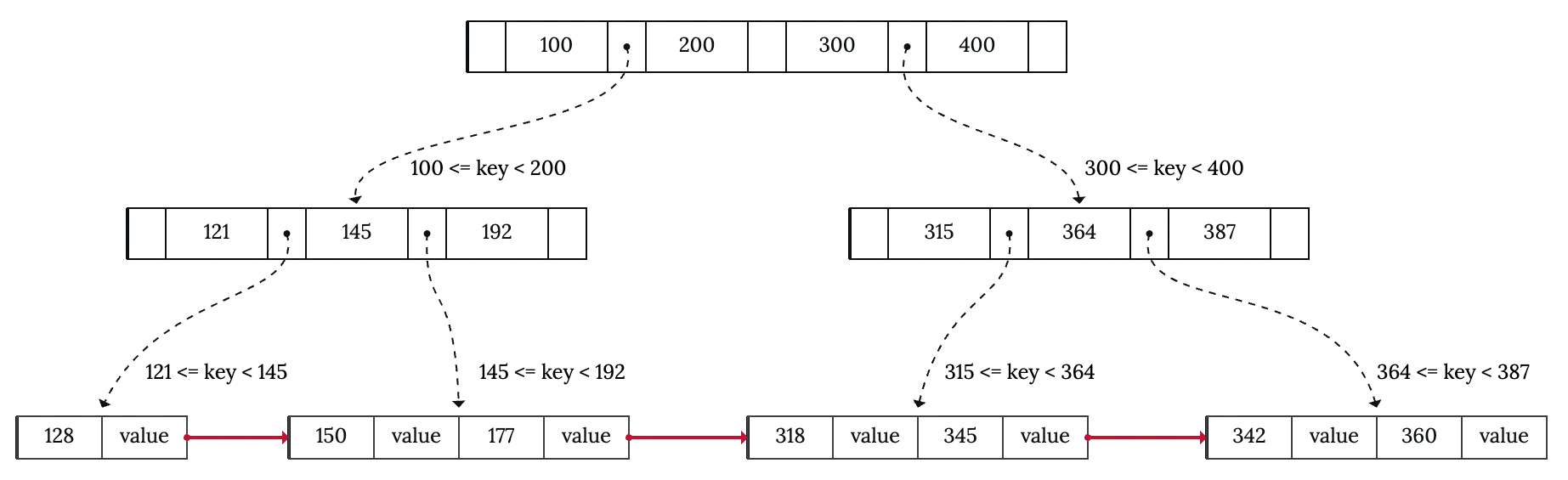
We mentioned B+ Tree in Part 1. The only difference is B+ Tree stores values only at the leaf nodes. The internal nodes only store separator keys, which serve as guide posts to find the correct leaf node.

At first glance, it seems like B+ Tree is doing more work. We still have to store every key and value, plus the extra separator keys, which would increase the size of the data structure. But the secret lies in how the “weight” of the tree is distributed.

Since internal nodes of B+ Tree don’t store values, they can fit more keys, thus having higher fanout. This would in turn make the tree wider and shorter compared to the original B-Tree. The majority of the tree size lies at the bottom layer, which contains all the leaf nodes. PostgreSQL says that: typically, over 99% of the tree size is from leaf nodes.

The shape of the tree, wide and short, coupled with the “heavy bottom” leads to two things:

1. The short height improves lookup performance because lookup complexity is proportional to the tree’s height.
2. The upper part of the tree (root node and internal nodes) is small. It can easily fit in cache (either database buffer pool or file system cache). This means that, often times, a lookup would incur only one cache-missed disk request to fetch the leaf node.

Another common improvement is linking leaf nodes together, forming a linked list, or even a doubly linked list. This makes range queries or key iteration simpler and more efficient, at a cost of increasing space consumption and maintenance logic (although not much). This trick is possible with B+ Tree since all keys are in the same level.

B* Tree

In The Art of Computer Programming, Volume 3, Donald Knuth discussed a variation of B-Tree and later named it B* Tree. The core idea of this variation is trying to delay splits as much as possible. Upon insertions, when a node is overflowed, instead of splitting, we prefer redistribute keys to sibling nodes if possible. When the sibling node is full, split both nodes into three nodes, each is 2/3 full.

This scheme improves the space utilization to 66%, which leads to better fanout and a shorter tree. Although I’m not sure about the performance trade-off for insertions. Does it negatively affect insert performance? According to Knuth: the insertion process gets slower because nodes tend to need more attention as they fill up.

Many database systems opt for B+ Trees rather than B* Trees, as B+ Trees offer a good balance of insert performance and query efficiency, especially for range queries, without the added complexity of B* Trees.

B-Link Tree (Lehman/Yao Tree)

Database implementations of B-Tree have to deal with the concurrency problem. Insert and delete are destructive operations and can interfere with lookup. Naive B-Tree is prone to race conditions. Consider this example:

One thread performs lookup and finds the leaf node containing the key. But before it can search within the node, another thread performs an insert, causing the node to split. By the time the first thread searches for the key, it won’t find anything since the key has already moved to a different node.

B-Link Tree proposes an extension upon the original design to tackle this problem. We need to make two adjustments:

1. Each node now stores an extra key, called high key (denoted with H:value in the image). The high key represents the biggest value the node can hold.
2. Each node maintains a pointer to the right sibling.

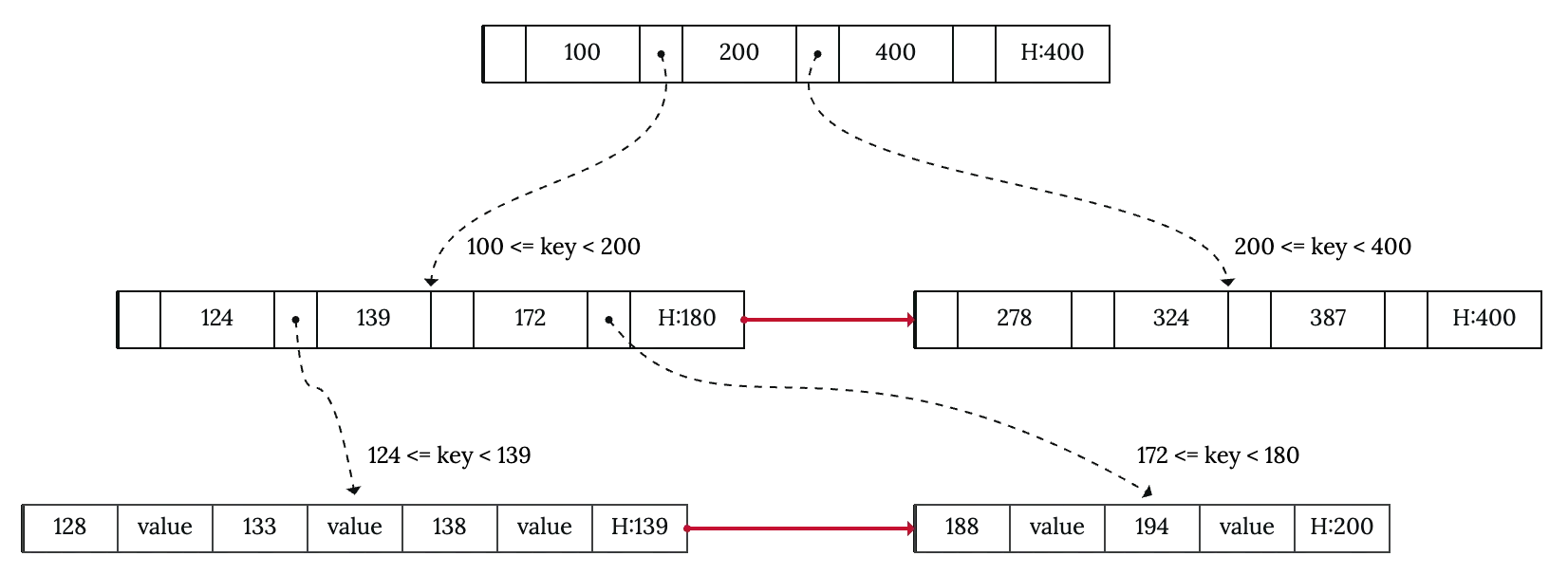
Let’s revisit the above race condition and see how B-Link Tree handles it:

Everything is still the same, up until thread 2 searches within the leaf node and finds no key. Remember the previous scenario? We stop the search here, but our key still exists in another node. We have no clue to answer the question: Does the key not exist, or is it moved to a different node? The high key will help us answer that.

• If the high key is bigger or equal to the key we’re looking for, it means that if the key does than, it must be in this leaf node. We stop the lookup and report the key is not found.
• If the high key is smaller than the key we’re looking for, it means that the key might move to sibling nodes due to node splitting. Now, we simply go rightward through the sibling pointers. The search stops when we either find the key or we reach the end.

With this scheme, insert will require at most three locks at any given time: the node to insert, the new split node, and the parent node. Lookup doesn’t need any locks, therefore isn’t blocked by insert.