Part 2

Databases

B-Tree is ubiquitous and appears everywhere, especially in the database realm. You can find a B-Tree implementation in almost every database nowadays, typically used for indexing. But why is that?

Data structure for disk

Low height

If you look at the anatomy of the lookup process of tree data structures (binary tree or B-Tree), there are two primary operations: comparison and pointer reference. At each level, you perform some comparisons to determine the next subtree. Then, you reference to the pointer to read the subtree.

The cost of comparison stays relatively constant, while the cost of pointer reference relies on the storage medium. Disk access is several orders of magnitude slower than memory access, making the cost of pointer references the dominant part. When designing data structures for disk-based storage, minimizing storage access is crucial. Often times, the number of storage accesses is proportional to the tree height. A data structure with low height is a desired property.

High fanout

Disk storage is represented as block devices. It organizes data into fixed-sized blocks (typically 4 KB), and each block has a unique address. Read and write operations are performed on entire blocks. Which means, to read/write a single byte, you must read/write the whole block containing it. This contrasts with character devices, which you can operate on byte or character level.

Let’s look at binary tree. With each pointer reference, we will read a node, which contains two children pointers. We can give a rough estimate of the node size: 128 bytes (a node value and two pointers). As we mention above, we must read the entire block (i.e. 4 KB). What should we do with the remaining bytes. How can we best utilize it?

One idea is to pack as much relevant data as possible into a single block. Relevant is a loosely defined term. Let’s say, two pieces of data, A and B, are relevant. If A is accessed, B is likely to be accessed soon after, and vice versa. We say that a data structure has better data locality if relevant data are placed in close proximity on the storage medium.

If the problem with binary tree is that it has too few children, how about we crank it up? A higher fanout leads to more keys per node, which can better utilize the disk block. Neighboring keys are relevant to each other, especially when performing range scan operation.

B-Tree is a good fit

To recap, we want a data structure with:

• Low height to minimize disk accesses.
• High fanout to improve data locality.

B-Tree checks both of these boxes. Also, B-Tree is a self-balancing structure, ensuring consistent performance for all operations. To maximize the I/O efficiency, the node size of B-Tree should align with block device size. For example, if the block size is 4 KB, the node size can be 4 KB (most common), or 8 KB, 16 KB, … (less common).

Another point in favor of B-Tree: It’s an ordered data structure. It can efficiently support range scan query, which is common in databases.

Modifications for databases

B-Tree is a good fit for databases. However, we need to make some adjustments to work in the database context.

Variable size records

In Part 1, we only talked about B-Tree with fixed-size keys and values. For databases, we need to handle variable-size data. Our current design has a few issues:

• We perform binary search to look for keys in the nodes. It won’t work if the key sizes are different.
• We should maintain the keys in sorted order. Keeping an array of different size elements sorted is a big hassle.

One solution a lot of database implementations employ is introducing a layer of indirection. We divide a node into two sections; one stores the keys and associated data, and the other stores the pointer to the keys. We also reserve some space for metadata about the node in the page header.

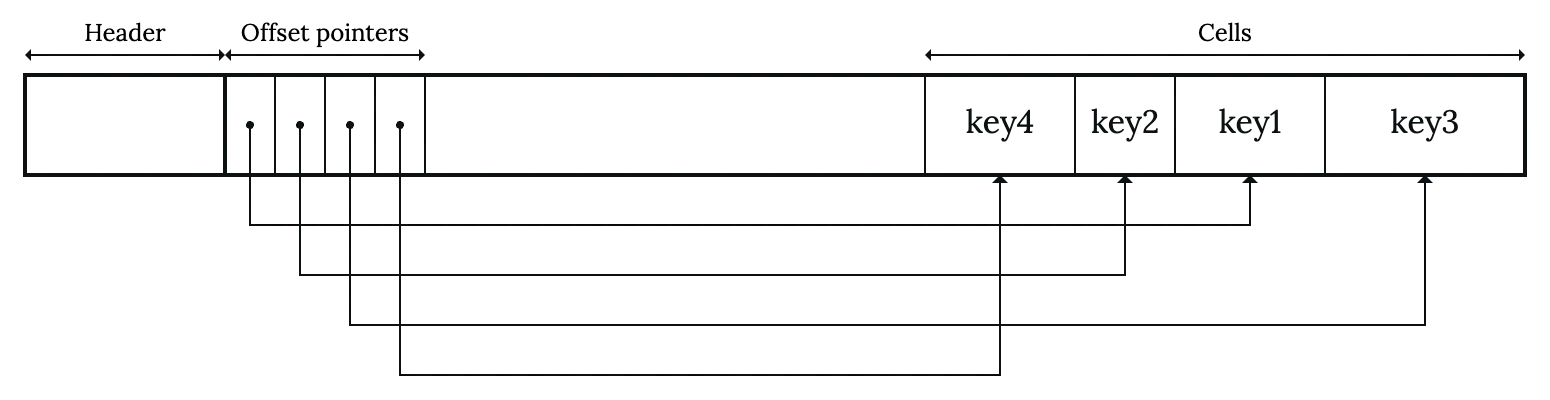
The pointers section starts from the left end. The cells section, where keys and associated data are stored, starts from the right end. The pointers store the byte offset of the cells. They’re analogous to the pointers in the traditional sense, but instead of pointing to a memory address, they point to a location on the node.

Let’s examine how the basic operations should update to adapt with this new change:

• Insert: Upon insertions, the pointers section grows to the right, whereas the cells section grows to the left. Remember, we need to keep the pointers section sorted, so after insert, some ordering is necessary. But luckily, the pointers are fixed size, so they’ll be easier to handle, and we don’t have to touch the cell section.

• Lookup: We still perform binary search as normal, but this time we need to follow the pointers to examine the keys.
• Delete: Delete is probably even easier. Just delete the pointer and shift all pointers behind backward. The cell can be left as-is and considered as free space.

There’s still a small caveat we need to take care of. When deleting cells, we leave some “holes” behind. These holes, while technically free spaces, can make the page fragmented and reduce the storage efficiency.

We can fix this in a few ways:

• Defragment the page by repacking the cells.
• Try to reuse free spaces when performing inserts.

The first option is too expensive to do on every insert. To amortize the cost, we can leave the holes to build up and perform a big repacking every once in a while (or have a background thread perform maintenance periodically). Reusing free spaces also helps but requires a mechanism to keep track of them (SQLite calls it the freeblock).

Concurrency

Databases must support concurrency accesses to B-Tree, both reads and writes. The current design is prone to race conditions.

Let’s start with the simplest solution: locks. Every time we want to modify a node, either insert or delete, acquire an exclusive lock on that node. It means writes will block reads. But there’s a catch: we also have to acquire locks for all nodes we traverse through in the path because we might need to modify those nodes as well. In another word, during insertions and deletions, one must acquire h locks, where h is the height of the tree. It can cause lock contention at the root node, which reduces concurrency.

B-link Tree, a variant of B-Tree, proposes a different way to approach this problem. PostgreSQL B-Tree implementation is based on this variant. We will discuss it further in Part 4.